Pattern recognition. In this section the standalone pattern recognition capabilities of the Forward Tracking Disks are put to the test. The combinatorial track finding algorithm is run on fully simulated event and the principal quality markers for pattern recognition are investigated. The principal detector design parameters related to pattern recognition - in particular the R-resolution, but also the material and the integration time - are varied to quantify their impact on the performance. Set-up The events are made up of tt signal plus a pile-up of 1 bunch-crossing of beam background for nominal machine parameters. The response of the detector is simulated in full detail using Mokka-GEANT4. The geometry is the nominal LDC FTD. The disk response in the simulation is fully efficient. The extrapolation of the track candidate to the next layer is performed using the propagator of the Pattern Recognition Toolkit described in the Tools section. It takes care of the proper estimation of the errors at the detector surface taking into account material effects (multiple scattering). As discussed before, a major challenge to the pattern recognition is formed by the abundance of very low momentum particles. To be fully realistic the pattern recognition aims to reconstruct particles down to a transverse momentum of 100 MeV. Simulated hits are digitized with a variety of assumptions on the technology. The principal parameter is the R-resolution of the disks. For the three innermost disks three values, each typical of a certain technology, are used: the 10 &mu m option corresponds to square pixels, 100 &mu m to macro-pixel technology and 1 mm is a typical resolution for double-sided strip detector stereo-measurement. Similarly, for the outermost disks four possible values are defined: the three listed before plus a fourth point with 3 cm resolution representative of 10 cm long single-sided strip detectors. Seeds for the track reconstruction are created using pairs of hits in the first two disks (inside-out track search). For the first extrapolation a broad beam constraint is used to constrain the trajectory. At each detector surface, compatible hits (considering the hit errors and the error on the extrapolated position) are searched. If a hit is found, it is added to the track stub and the trajectory state is updated using the Kalman filter formalism. This procedure is iterated until no compatible hits are found or the end of the tracker is reached. Results The pattern recognition performance of the standalone FTD is discussed on the basis of measurements of three quality markers. Extrapolation precision One of the principal ingredients of pattern recognition is the precision with which a track candidate can be extrapolated to each next layer. This precision determines the search window within which hits are compatible with the track. In this subsection, quantitative estimates of the extrapolation error are given. As illustrative examples, in the figures below the error on the predicted position on disk 4 (leftmost figure) and disk 6 (rightmost figure) is shown as a function of particle momentum. For this example the first three FTD disks are equipped with pixel detectors providing 10 × 10 &mu m2 space point resolution, while the four outermost disks have single-sided strips with virtually no R resolution: the space point resolution is given by 10 &mu m × 3 cm. The dependence of the extrapolation precision on particle momentum has the familiar a &oplus b/p form. The multiple scattering contribution - proportional to 1/p - dominates for low momentum tracks up to approximately 5-10 GeV. For larger momenta the extrapolation uncertainty remains constant. 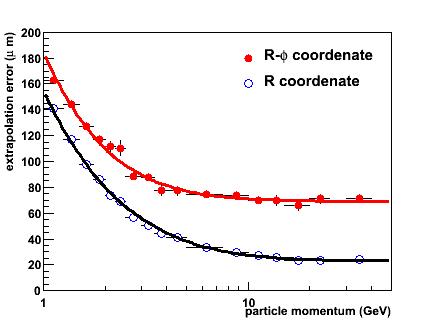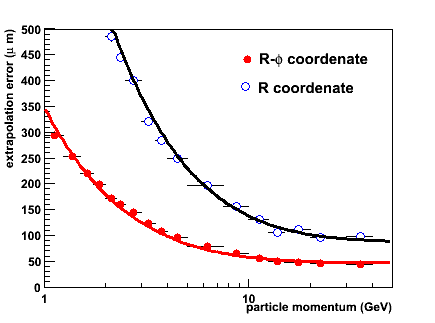When comparing the uncertainty on the R &phi (in the bending plane of the magnetic field) and R coordenates, some differences become clear. When extrapolating the track state measured on a triplet of hits to the fourth disk (leftmost figure) the track momentum is only very roughly measured. This uncertainty works through in the extraoplation precision: even though the distance to the fourth disk is rather small (11 cm) compared to the spacing between disks 4-7 (25 cm) the uncertainty on R &phi is between 80 and 180 &mu m. The R coordenate is much better constrained (in the Rz view the projected helix forms a straight line which is very well constrained by three precise measurements). In the rightmost figure, the situation in the sixth disk is shown. The extrapolation in this case is over a much larger distance: 25 cm instead of 11 cm. The momentum is now much better constrained, leading to a much smaller uncertainty on the R &phi coordenate for high momentum tracks. This beneficial effect is countered by the material of the outermost disks leading to a larger error due to multiple scattering. For the R-coordenate the precision is much degraded as a result of the worse resolution of the outermost measurements. In the four figures below the area of the average extrapolation error ellipse on the consecutive detector layers is shown. Four different options are considered. The upper, leftmost figure corresponds to a setup with 3 pixel disks + four DS strip disks. In the upper, rightmost figure the pixel disks have been replaced by macro-pixels. In the lower, leftmost figure, all seven disks are equipped with DS strip detectors. Finally, in the lower, rightmost figure, the first three disks are equipped with DS strip detectors and the outermost four disks have SS strip detector. In all cases, the first extrapolation suffers from the weak beam constraint. Therefore, the search window area at FTD layer 3 is largest. The second extrapolation over a relatively short distance, to layer 4, is much more precise, as now three precise space points are available to constrain the trajectory. The last three extrapolations benefit from the improving precision of the track parameter estimate, but suffer from the large distance (25 cm) between layers. 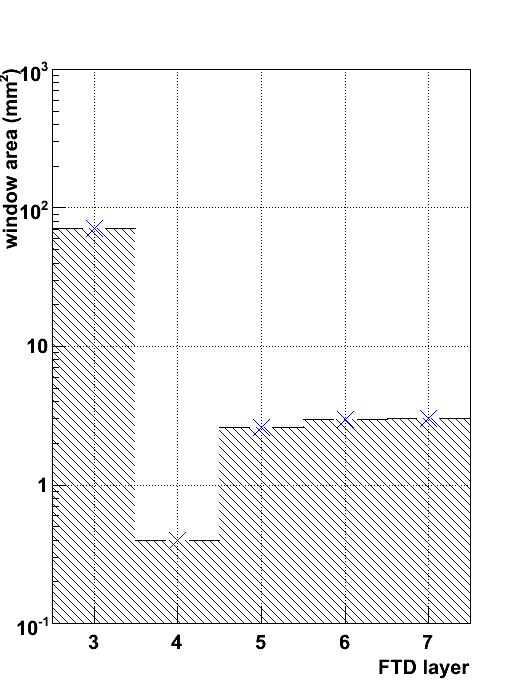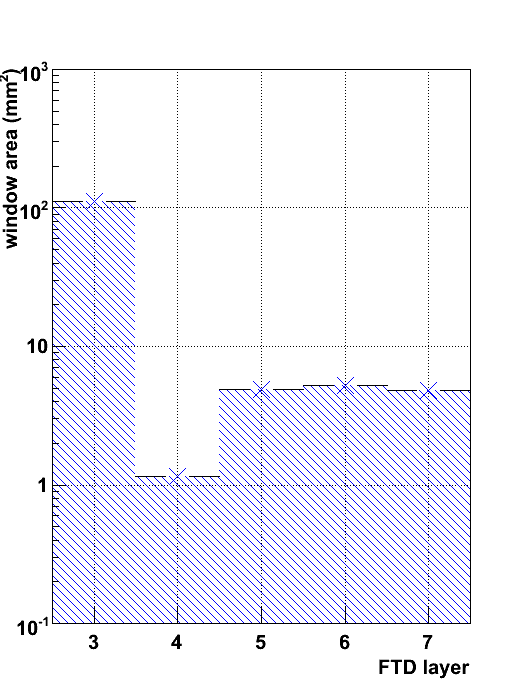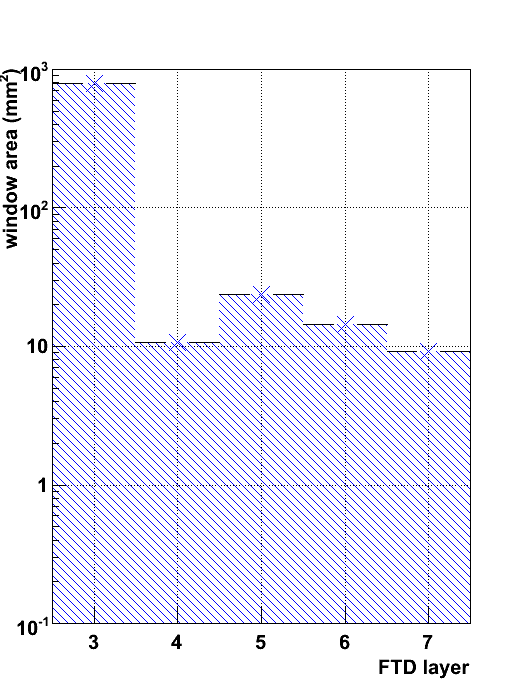The difference between the setup with the most precise (10 &mu m in the first three disks and 1 mm in the last four) R measurement and the least precise one (1 mm in FTD 1-3, a few cm in FTD 4-7) is naturally quite signficant. For the least precise technology the underdetermination of the trajectory in the non-bending plane in the latter leads to a factor 10 increase in the search window area. Local confusion: number of compatible hits The principal local quality marker for pattern recognition is the number of compatible hits in each layer found by the track candidate. 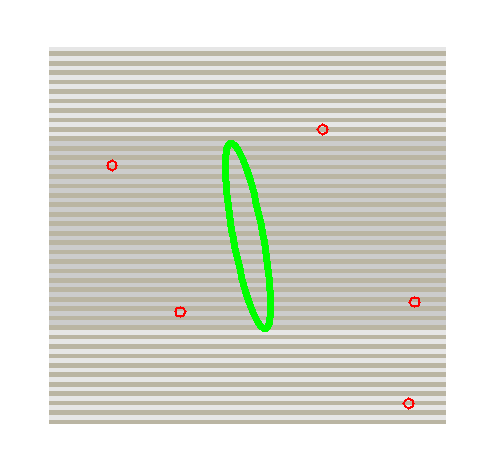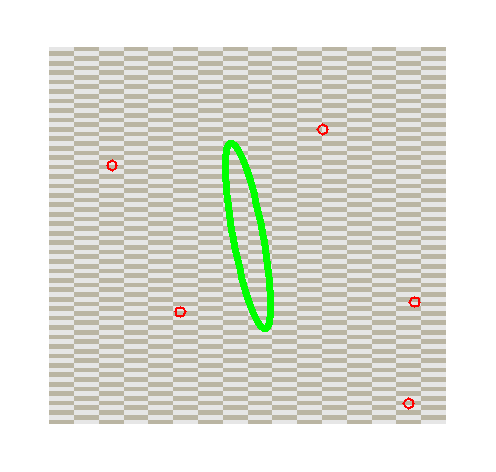The number of compatible hits naturally depends on the uncertainty with which the track candidate is extrapolated to the layer, the local hit density and the hit error. The dependence on the detector technology is clarified through an example in the figures below. In both figures a search window is indicated as a green ellipse. The underlying technology is indicated schematically: the leftmost figure represents a single-sided strip detector, while the rightmost figure corresponds to rectangular pixels. The dark grey area in the leftmost figure indicates the compatible area. Thus, multiple non-related hits (red circles) may lead to ambiguities in one technology, whereas this additional confusion is avoided in the more granular pixel technology. In the figures below, the average number of compatible hits - the local source of ambiguity - is shown for the different tracking disks. 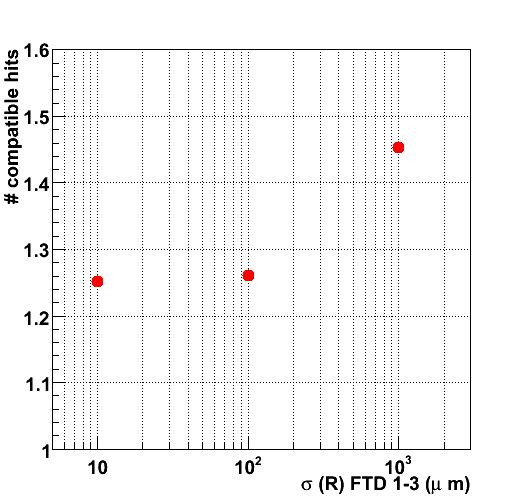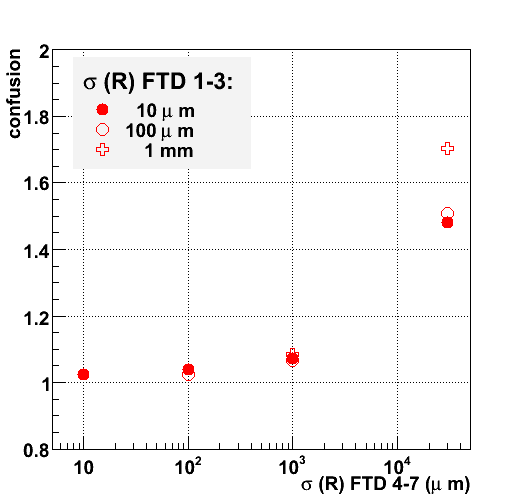The upper and leftmost figure corresponds to the third disk. Pairs of hits are extrapolated to the third disk with the aid of a loose beam constraint. The track parameters are only weakly constrained. The search windows are therefore quite large and the probability to find multiple compatible hits is non-zero. The three points correspond to three different resolutions in the R-coordenate: 10 &mu m (pixels) 100 (&mu m) macro-pixels and 1 mm (stereo-measurement of double-sided micro-strips). All other parameters are kept fixed. The performance of the first and second setup are quite similar, the average number of hits is 1.25 and 1.26, respectively. The micro-strip setup has considerably worse performance: due to the reduced resolution the R-constraint is not as effective in avoiding confusion. 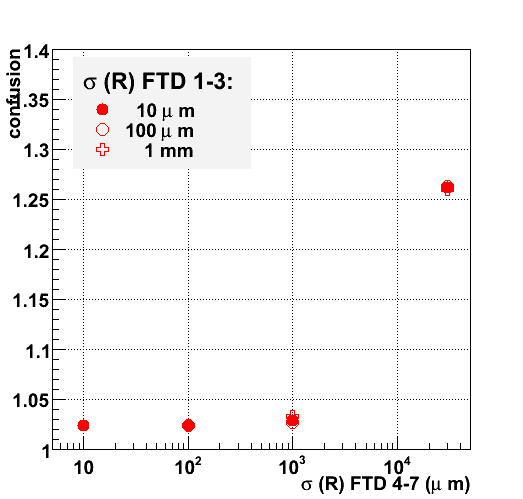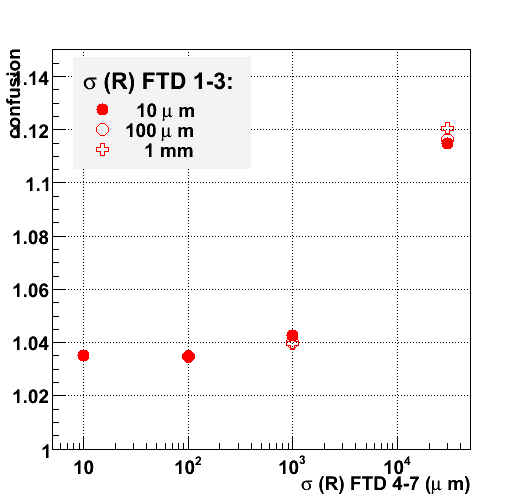The figures 2 through 4 present the average number of compatible for the consecutive disks. The 3 options for the first three disks are complemented by 4 options for disk 4-7. The convergence of the pattern recognition is clearly visible: the number of compatible hits approaches 1 as more layers are added. The level of ambiguity at the fourth disk is reduced dramatically compared to that in the first three disks. The stronger constraint on the track candidate together with a short the extrapolation distance yield a very small search window. As a result, for a large majority of track candidates only one compatible hit is found: the average number of compatible hits is approximately 1.02. This is true for all technology options of the final four disks, except for single-sided strips. In this case, the level of confusion drops only very slowly: new ambiguities keep arising at considerable frequency until the last layer. The number of candidates The third marker studied is the number of reconstructed tracks compared to the number of simulated tracks. Clearly, a value of 1 indicates convergence. 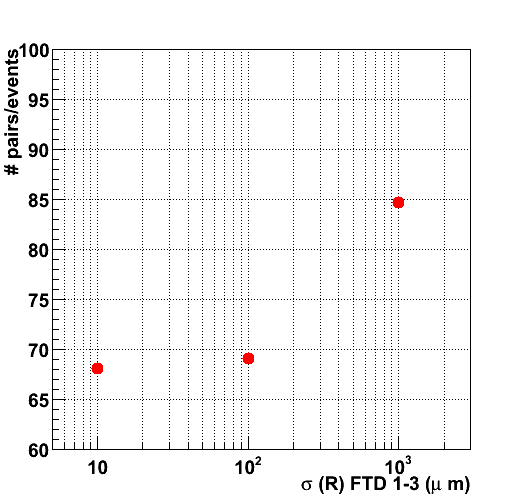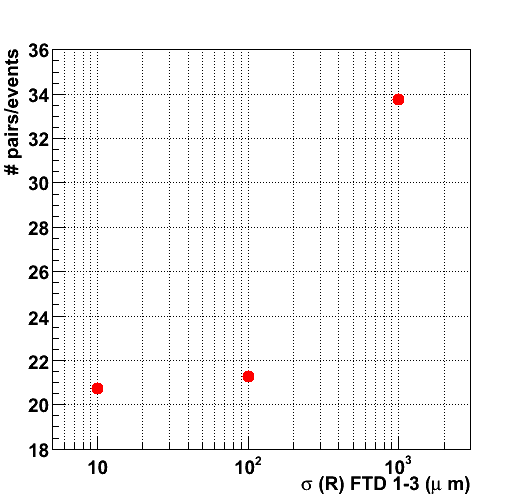In the figures below the results for the seed-generation step are shown for three assumptions on the R-resolution of the first disks. In the leftmost figure the number of hit pairs (leftmost figure) and triplets (rightmost figure) compatible with a track model within the constraints (pT < 100 MeV, |cos( &theta )| > 0.83 ). Even for the square-pixel set-up, the number of pairs is of the order of 70./event, well in excess (by a factor 10) of the number of charged particles in the forward tracker (~6.7). The number of hit pairs fluctuates strongly: for dense events it increases roughly as the square of the number of tracks. Clearly, the combination of two 2D space points and a loose beam constraint is not sufficient to constrain the fit. The two set-ups with pixel and macro-pixel detectors have a very similar performance, while for the micro-strip option, the confusion increases by 30 %. Addition of a third measurement (see the rightmost figure) leads to a reduction of the confusion: the average number of triplets (21) exceeds the number of charged tracks by "only" a factor 3. At this point, the measurement in the bending plane is still hardly a constraint. The improvement in the confusion is nearly entire due to the constraint of the track model in the R-z plane. The 10 &mu m and 100 &mu m resolution yield similar results (the search window is of that order even for the best resolution), but the 1 mm option has considerably larger confusion. In the four figures below, the number of reconstructed tracks with at least four, five, six and seven hits is shown for different assumptions on the technology. The numbers are normalized to the number of charged particles leaving the same number of hits: a confusion of 1 implies that all tracks are reconstructed, with no fakes. Clearly, with the addition of more measurements the level of ambiguity decreases: for 4-hit tracks the fraction of fakes is still significant (20 %), for 5, 6 and 7-hit tracks the level drops to 10 % and below for the best performing technologies. 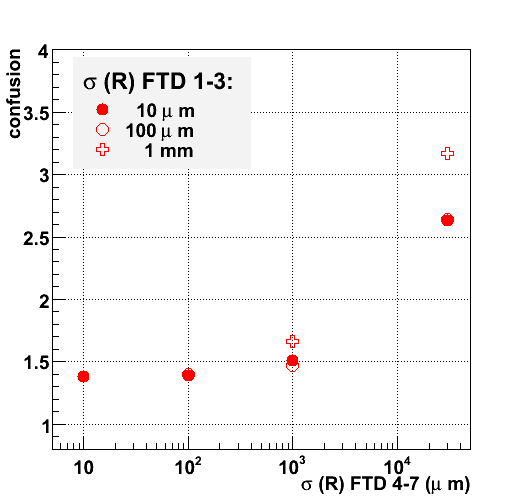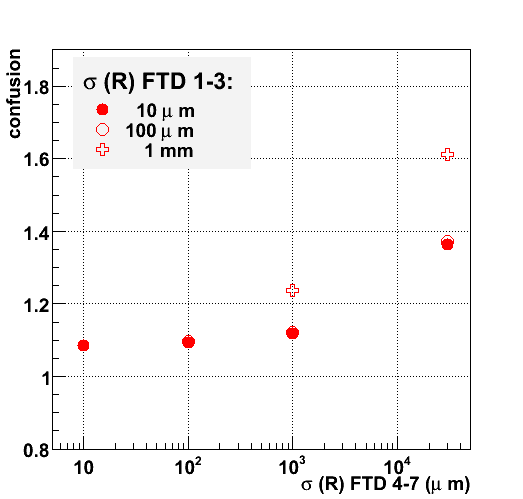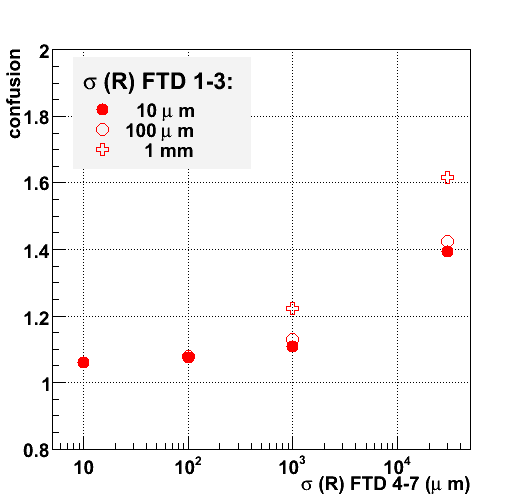A striking result is the lack of convergence for the single-sided strip option in the outermost four disks (the rightmost points in the figures): even in combination with a 3-layer pixel detector the initial confusion is not fully resolved even for 7 measurement points. Much better performance is obtained if the four outermost disks rely on double-sided silicon micro-strip detector technology (the third column of measurements in the figures). For a Forward Tracker that relies entirely on double-sided silicon micro-strips (the results are indicated by a star in the third column) there is still considerable ambiguity after four layers: only after six or seven layers the performance becomes comparable to the best performing setups. If the double-sided micro-strip detectors in the outermost disks are combined with a more granular - pixel or macro-pixel - detector in the first three disks the performance becomes quite comparable to that of the most granular setups. Five space points are sufficient to ensure convergence to a confusion of slightly over 10 %. Clearly, even better results are obtained if the first three disks are equiped with the most granular detector technologies. The performance of three setups - with 7 pixel layers, a combination of 3 pixel layers and four macro-pixel layers and a detector consisting of 7 macro-pixel layers - are indicated in the two leftmost columns of each figure. At this point, the dependence of the pattern recognition performance on cell size becomes quite weak. Material The material in each layer has an effect on the pattern recognition through the multiple scattering contribution to the track parameter estimate and the size of the search window. To estimate the effect in a quantitative way, for one setup (macro-pixels + double-sided micro-strips) the simulation is repeated under extreme assumptions. In the first steps a rather challenging assumption of 1.2 &permil X0/layer is applied to the first three disks. This yields a very significant improval of the performance. The triplet rate drops by 10%. The fake rate for the four-hit trajectories decreases even more (by 23 %) yielding a very clean (1.02) track sample with only four layers to constrain the trajectory. Under these conditions, a similar reduction of the material in the outermost four layers has a negligible effect. The effect of an increase in the material budget is evaluated by repeating the simulation with a material budget of 12 % X0/layer. The pattern recognition performance in these conditions - corresponding to the worst-case scenario - breaks down completely. The initial number of seeds increases by over a factor 2. No convergence is reached: a fake rate greater than 100 % persists even after the algorithm reaches the final layer. Read-out time The background levels in the forward tracker require fast read-out of the detector. Ideally, the detector should be able to unambiguously identify the bunch crossing of each hit. This is what has been simulated above. To estimate the effect of longer integration times, samples have been created containing hits from a signal tt event plus hits from the machine background in nominal corresponding to a number of bunch crossings. The study of the pattern recognition markers is repeated for one setup (macro-pixels + double-sided micro-strips). Instead of a single bunch crossing, the first three disks integrate background from 10 bunch crossings. The material of these disks is reduced to 1.2 &permil/disk. Disk 4-7 still distinguish separate bunch crossings. In the case of 10 integrated bunch crossings the pattern recognition evolves as follows: The number of hit pairs in the first two disks (compatible with the trajectory constraints) increases dramatically: on average over 2000 pairs/event are found (was 70 for the same setup integrating a single bunch crossing). Addition of a third hit leads to a signficant reduction: 108 triplets are found per event compared to 20 for a single bunch crossing. In layer 4, 5, 6 and 7 (the disks that have single bunch crossing read-out) the local confusion (average number of compatible hits) returns to its usual value between 1.05 and 1.02. The pattern recognition now rapidly converges to a fake rate of approximately 25% in the fourth disk and down to a few % in the subsequent disks. The performance depends critically on the material budget: for a 1.2 %/disk material budget and 10 integrated bunch crossings, the measurement in the third and fourth layer are much less efficient in reducing the number of fake candidate. An average triplet multiplicity of 350 is found. At the fourth layer 4.4 candidates/track remain, the probability of multiple compatible hits is 10 %. The fake rate remains as high as 40 % throughout the pattern recognition stage. Discussion In this section, the pattern recognition performance of a stand-alone forward tracker has been evaluated in realistic conditions. For fully simulated dense signal topologies plus the underlying machine background a state-of-the-art pattern recognition algorithm is run on the standalone FTD. Three principal markers of the pattern recognition performance are determined: the extrapolation precision, the number of compatible hits (the local confusion) and the final number of candidates (the final confusion). Thus, the impact on the performance of a a range of detector technologies - from highly granular pixel detectors to the essentially one-dimensional measurements of single-sided micro-strip detectors - has been established. The essentially one-dimensional measurements of single-sided micro-strip detectors provide insufficient constraints for the pattern recognition in dense events. The next option considered is that of double-sided micro-strip detectors with modest stereo-resolution for the R-coordenate. The R-measurement leads to a considerable improvement of the pattern recognition performance. The pattern recognition performance is found to be adequate for the outermost disks. For the most demanding region of the forward tracker, granular (macro-) pixel detectors provide a clear advantage. The combination of low occupancy, precise extrapolation of track candidates and small hit errors forms a powerful constraint. This allows to keep the initial ambiguity - the number of doublets and triplets - as small as possible and ensures rapid convergence of the stand-alone pattern recognition. While more granular detectors naturally provide better performance, reduction of the R-resolution to far below the extrapolation precision leads to a marginal improvement. Therefore, the square pixel option and rectangular macro-pixels provide quite similar performance. The material budget reveals itself as a critical parameter for the pattern recognition of low momentum tracks. Only a very challenging material budget allows to keep the compatible windows of such tracks small enough. The read-out speed of the innermost detectors is of utmost importance. While convergence of the pattern recognition has been demonstrated for 10 integrated bunch crossings, the performance will inevitably degrade for longer integration times. Home Next Article