Tools. The simulation and reconstruction of events in Tools - fast simulation The term "fast simulation" refers to any simulation tool that avoids the tedious and slow simulation - in GEANT or similar packages - of the interactions of the particle with the detector material. In most fast simulation packages, the detector model (digitization) is simplified (usually hits are smeared with a Gaussian resolution function). The packages used here are furthermore limited to the response of a single particle, ignoring the complications that arise due to imperfect pattern recognition. Finally, the level of complexity of the geometry is an order of magnitude less than in the "full simulation" of a running experiment. Fast simulation packages thus determine an ideal performance: the response of the detector will tend to the fast simulation response. While thus limited in scope, the fast simulation packages used here are quite sophisticated. Some of them have been around for years and were tested extensively against the response of collider experiments. They have proven a valuable tool for the fast and flexible mapping of instrumentation effects. SGV Simulation a Grande Vitesse was developed by Mikael Berggren in the Delphi collaboration. In over a decade it has been extensively tested. The simplified detector geometry is described as cylinders with a common axis, parallel to the magnetic field, and as planes perpendicular to the common axis. The geometries can be stored and read back from a human-readable ASCII file. SGV is a machine to calculate covariance matrices: For each charged particle generated by the bare physics simulation (which can be selected at will by the user) which is either stable or decays weakly, SGV calculates which of the tracking detector surfaces the track helix intersects. From the list of those surfaces, the program analytically calculates the precision with which the parameters of the track can be measured. This calculation includes the multiple scattering in the traversed surfaces, and the measurement precision at each surface that measures the track position. It takes the spiraling of low pT charged tracks in the magnetic field into account, as well as the dependence of the point-resolution on the angle of incidence of the tracks on silicon detectors, and on drift length in long-drift gaseous detectors. Precise formulae for multiple scattering are used, taking the rest mass of the particles into account. The production vertex can be chosen to be at any position in the detector, and the decay length can also be freely chosen. To generate the initial event, interfaces to PYTHIA, JETSET and SUSYGEN are included in SGV. Single particle "ray gun" simulation is also included, as is the reading of generated events form an external file. The reconstructed particles can be analyzed in a separate part of the program. Alternatively, the result can be output in a format based on LCIO, developed by B. Jeffery at Oxford. Further information can be found following this link . LicToy This new package for flexible and fast detector optimization has been developed by a team of people (M. Valentan, M. Regler, W. Mitaroff) at HEPHY Vienna. It is an integral part of the ILC simulation effort of the SiLC collaboration. The detector model corresponds to a generic collider experiment with a solenoid magnet, and is rotational symmetric w.r.t. the beam axis; the geometric surfaces are either cylinders ("barrel region") or planes ("forward/backward region"). The magnetic field is homogeneous and parallel to the beam axis, thus suggesting a helix track model. Material causing multiple scattering is assumed to be concentrated within thin layers. The simulation generates a charged track from a primary vertex along the beam axis, performs exact helix tracking in a homogeneous magnetic field with inclusion of multiple scattering, and simulates detector measurements including inefficiencies and errors. The simulated measurements are then used to reconstruct the track by fitting its 5 parameters and 5x5 covariance matrix at a given reference cylinder, e.g. the inside of the beam tube (they may be converted to a 6-dimensional Cartesian representation). The method used is a Kalman filter, with the linear expansion point being defined by the undisturbed track at that surface. Subtle tests of goodness of the fits, like chi-square distributions and pull quantities, are standard. An integrated graphics user interface (GUI) is available. The algorithms used in the tool are on a solid mathematical base. The program is written in MatLab®, a high-level language and IDE, and is deliberately kept simple. It can easily be adapted to meet individual needs; for an expert this would take only a couple of hours. A number of documents describing the package, and containing instruction to use it, is linked below: Presentation Report User Guide LCDTRK Developed by Bruce Schumm (UC Santa Cruz). This program calculates covariance matrices with which to smear tracks. It outputs the covariance matrix for the five track parameter is determined as a function of momentum and tan (&lambda). The covariance matrices are built - using the Billoir method - from a description of the detector which includes the geometry, the material, and the expected measurement uncertainties of the tracking detectors. a description on teh SLAC confluence page. a tar file containing the source code. CMS Kalman filter tool kit For most of the resolution studies reported in this study, a Kalman filter tool kit implemented in object-oriented C++ code, has been used. It is based on the CMS track reconstruction software (thanks to Tomasso Boccali for authorisation to re-use this software). The code has been extracted into a series of libraries that can be used stand-alone or in the MarlinReco framework. The tool-kit comprises a sophisticated track propagation model - containing the deviation of the charged particle trajectory by magnetic fields of arbitrarty complexity. The interaction with thin layers - multiple scattering and energy loss - are taken into account by the propagator. Given a trajectory state (a set of measurements fully describing the particle parameters and their errors) a new trajectory state with correctly transformed errors can be predicted on any detector plane. Tracker hits are represented as 2D measurements on a plane. If a compatible hit is found on the plane, the hit may be added to the track. The trajectory state is updated to take into account the newly added information through the Kalman Filter formalism. 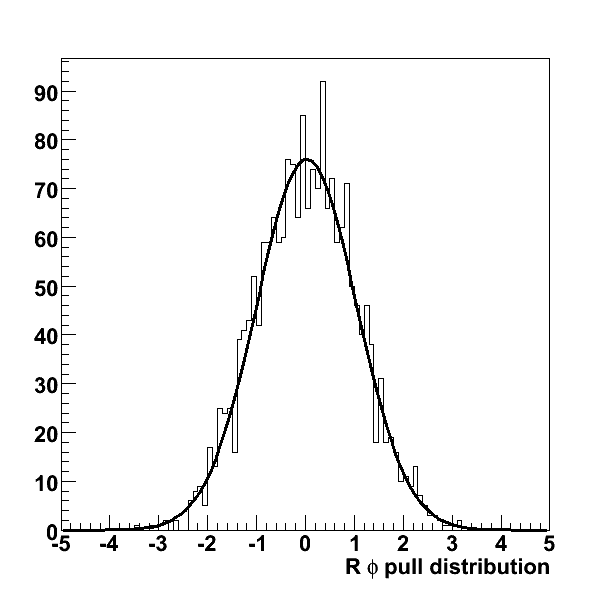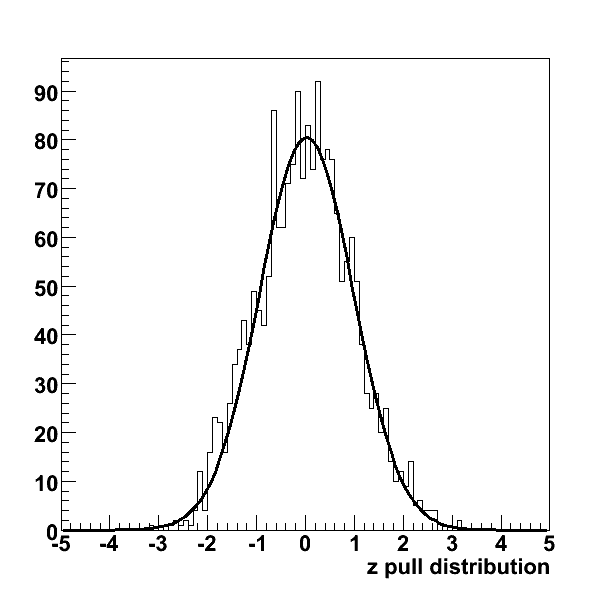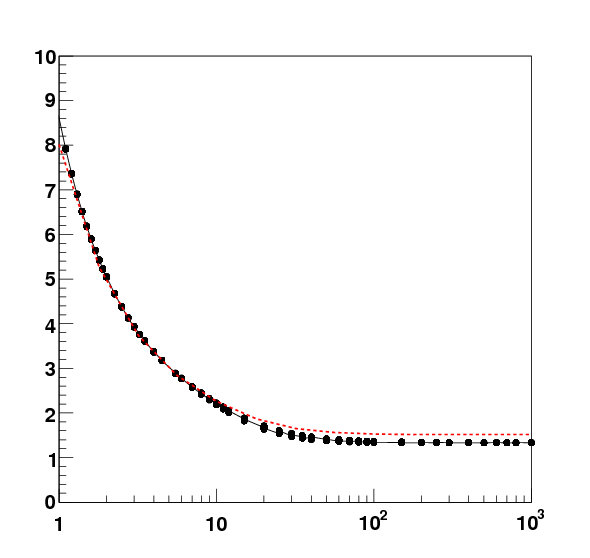While the original CMS code has been thoroughly validated against large Monte Carlo samples, several pieces of code - the LCIO format of the hits, the interface to the LDC geometry in GEAR - are new. Therefore, the package is thoroughly tested. Internal consistency is demonstrated by the pull distributions below. 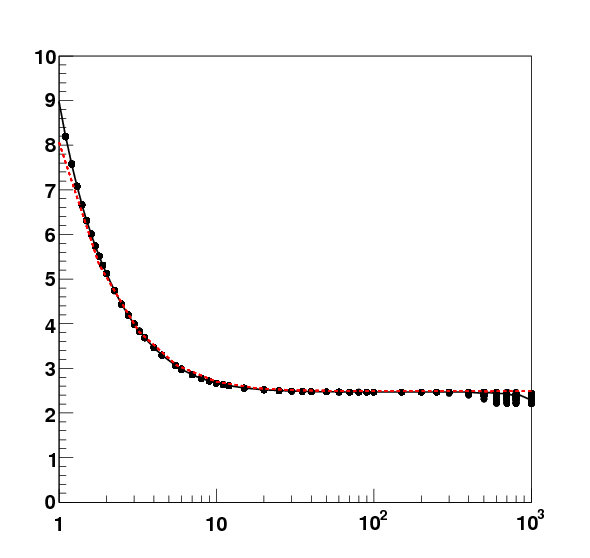Correctness of the predictions of the model is further tested by comparing with the principal fast simulation tools on the market. Predictions for the resolution of all track parameters on a variety of toy models have been compared to LiCToy, LCDTRK, SGV. In no cases were signficant deviations observed. In the figures below the predictions of the KF tool kit (black points) and LCDTRK (red dashed line) for transverse (leftmost figure) and longitudinal (rightmost figure) impact parameter resolution as a function of track transverse momentum is shown. The detector model in this case is a toy geometry considering only tracks at a polar angle of 90 degrees consisting of 5 vertex detector and two tracking layers (more or less disposed as the VTX and Silicon Intermediate Tracker layers in the LDC) in the Tools - full simulation The study of pattern recognition performance requires quite sophisticated software. In particular, as pattern recognition inherently deals with complex multi-track topologies, the fast simulations tools discussed before cannot be employed here. In this study, top pairs produced at a center-of-mass energy of 500 GeV/c are taken as a benchmark sample. To study pattern recognition interactions with the detector are necessarily taken into account. Therefore, the generated particles are tracked through a detailed detector geometry using GEANT4. For this study, the LDC detector geometry (LDC01Sc) in Mokka is considered. As discussed in the section on machine backgrounds, hits resulting from beamstrahlung play an important role in the forward tracker. Therefore, fully simulated background hits corresponding to a number of bunch crossings (1-20) are superposed on the signal events. Tools - reconstruction The reconstruction of the fully simulated events is perhaps the most critical issue here. Previous experiments - and those of the LHC about to start data taking - have developed elaborate software packages. One may argue that the full pattern recognition potential of the detector (the hardware) can only be explored using a truly state-of-the-art algorithm (the software). The software of the International Linear Collider - while making considerable progress - is probably not quite at this level. The full simulation results presented in this study rely on the baseline global track reconstruction of the Large Detector Concept. The FullLDCTracking algorithm combines the track stubs reconstructed by the LEPTracking algorithm in the gaseous barrel detector (Time Projection Chamber). As the name suggests, the LEPTracking algorithm was developed for track reconstrucion in the DELPHI Time Projection Chamber. The SiliconTracking algorithm tries to resolve patterns in the vertex detector, the Silicon Intermediate Tracker and Forward Tracking Disks. The two track collections are merged taking care of doubly reconstructed tracks. Pattern Recognition ToolKit In the main body of the study on pattern recognition a much simpler problem is tackled. The complexity of the pattern recognition problem is reduced by considering only one detector region: hit patterns are searched for only within the Forward Tracking Disks. Throughout the pattern recognition process, propagation (extrapolation) and updating of trajectory descriptions are done using the tools provided by the Kalman filter kit described before. Thus, at all stages the fit to the trajectory (and its errors) yields an optimal estimate given the available information. In the FTD stand-alone study a simple, but extremely powerful algorithm is employed. The combinatorial algorithm is one of the most popular approaches on ther market: it is the baseline pattern recognition algorithm of both ATLAS and CMS (see ). The combinatorial track finder starts off with a collection of seeds. Typically, hit pairs + beam constraint or triplets in high-granularity, low-occupancy detectors are chosen. For each seed the weakly constrained track model is extrapolated to the following layer. In this layer, compatible hits are searched for. For each compatible hit, a copy of the track candidate is made and updated with the hit information. All candidates are in turn propagated to the next layer, where the process is repeated. The iterations for a given candidate are only stopped if no more compatible hits are found (in actual implementations the stopping conditions are more complex to deal with layer inefficiencies). The strenght of the combinatorial algorithm is that it does not try to resolve ambiguities locally, with the limited information it has available. Instead, the track candidate is split and each copy is given a chance to accumulate further hits. Effectively, the decision is postponed until the information from more tracking layers is available. Naturally, the initial weakly constrained track candidates have a high probablity of picking up spurious hits. This "combinatorial explosion" of track candidates is countered by the mortality of "wrong" track candidates that find no further compatible hits. If sufficient constraints are supplied the algorithm converges to an efficient and clean set of tracks. For this study, the algorithm is run "inside-out", i.e. starting from seeds created by combining hits in the innermost forward tracking disks and working its way towards the outermost disk. The choice of this algorithm - while well founded - remains a bit arbitrary, as is the decision to run it "inside-out". It would certainly be interesting to compare the current results with those obtained by other approaches. Home