Contents
Práctica sobre el MODELO DE LORENZ-HAKEN (1b)
Programa traducido de Mathematica a Matlab y comentado por Fernando Hueso González. Óptica cuántica (Seminarios de teoría semiclásica y simulaciones) - 4º de Grado de Física, 31 de mayo de 2011.
global s b r syms d s b r format compact % Solución estacionaria (analítica) d = 1; P = sqrt(r-1); F = sqrt(r-1); solestac = [d,P,F]; % Estabilidad lineal (hasta bifurcación de Hopf rHB) rHB=-s*(3+b+s)/(1+b-s);
a) Estabilidad lineal (condiciones iniciales próximas a la solución estacionaria)
s=3; b=1; r=5; Tfin=300;
RHB=subs(rHB)
Solestac=subs(solestac), F0=subs(F), P0=subs(P), d0=subs(d)
h=0.05; t=0:h:Tfin; %Define el paso h que utiliza Runge-Kutta
RHB =
21
Solestac =
1 2 2
F0 =
2
P0 =
2
d0 =
1
Cambio adiabático
La primera vez que se ejecute este bloque hay que haber ejecutado antes el anterior. Después ya sólo hay que repetir este cambiando únicamente el valor de r.
r=15; [t,solnum] = rungekut('laser',t,[F0,P0,d0]); clc%Limpia pantalla F0=solnum(end,1), P0=solnum(end,2), d0=solnum(end,3) tmin=0; tmax=Tfin; nmin=find(t>=tmin,1,'first'); nmax=find(t<=tmax,1,'last'); close all titul='Cambio adiabático'; figure('Name',titul),plot(t(nmin:nmax), solnum(nmin:nmax,1).^2); title(titul), xlabel('t'), ylabel('F^2')
F0 =
3.7417
P0 =
3.7417
d0 =
1.0000
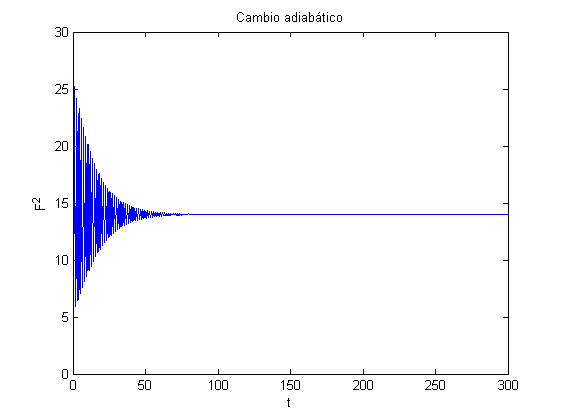
Se observa que para obtener el método de cambio adiabático, redefinimos F0, P0 y d0 en el bloque anterior una vez se ha calculado rungekut. La idea es iterar el bloque anterior varias veces variando r poco a poco, para no saltar demasiado y salirse de la línea estacionaria. Por contra, en el próximo bloque, hard-mode excitation, haremos justo lo contrario, separarnos notablemente en condiciones iniciales de la solución estacionaria para caer en las soluciones caóticas.
b) Hard-mode excitation -> biestabilidad generalizada
s=3; b=1; r=20; F0=0.001; P0=0.001; d0=0.001; Tfin=500; h=0.05; t=0:h:Tfin; [t,solnum] = rungekut('laser',t,[F0,P0,d0]); tmin=0; tmax=Tfin; nmin=find(t>=tmin,1,'first'); nmax=find(t<=tmax,1,'last'); close all titul='Hard-mode excitation' figure('Name',titul),plot(t(nmin:nmax), solnum(nmin:nmax,1).^2); axis tight, title(titul), xlabel('t'), ylabel('F^2')
titul = Hard-mode excitation
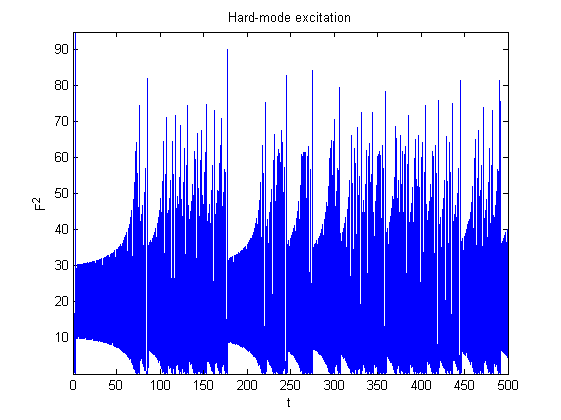
Representación de atractores
s=3; b=1; r=26; Solestac=subs(solestac) Tfin=100; h=0.02; t=0:h:Tfin; F0=15;P0=0.01;d0=1; [t,solnum] = rungekut('laser',t,[F0,P0,d0]); tmin=0; tmax=10; nmin=find(t>=tmin,1,'first'); nmax=find(t<=tmax,1,'last'); close all titul='Representación de atractores 2D'; figure('Name',titul),plot(solnum(nmin:nmax,1), -solnum(nmin:nmax,3)); title(titul), xlabel('F'), ylabel('-d') titul='Representación de atractores 3D'; figure('Name',titul),plot3(solnum(nmin:nmax,1), solnum(nmin:nmax,2),-solnum(nmin:nmax,3)); title(titul), xlabel('F'), ylabel('P'), zlabel('-d')
Solestac =
1 5 5
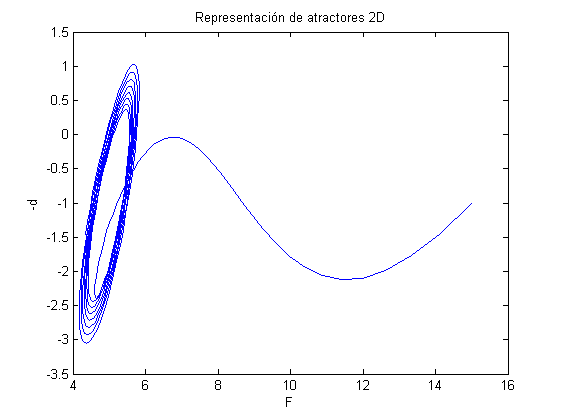
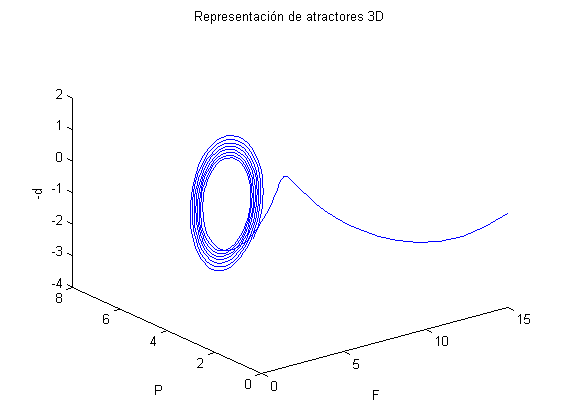
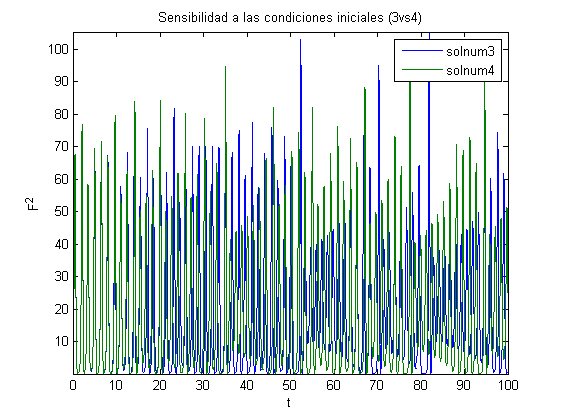
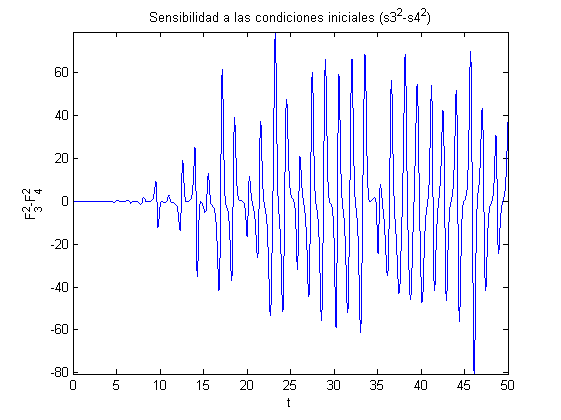
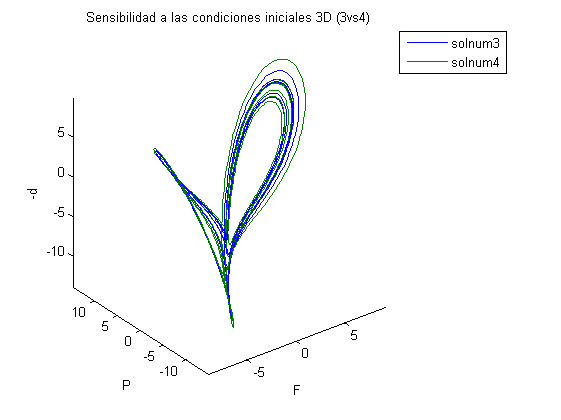
Comprobación Sensibilidad a las Condiciones Iniciales
s=3; b=1; r=23; Tfin=50; h=0.05; t2=0:h:Tfin; [t2,solnum2] = rungekut('laser',t2,[1,1,1]); F0=solnum2(end,1); P0=solnum2(end,2); d0=solnum2(end,3); Tfin=100; h=0.01; t3=0:h:Tfin; t4=0:h:Tfin; [t3,solnum3] = rungekut('laser',t3,[F0,P0,d0]); [t4,solnum4] = rungekut('laser',t4,[F0+0.01,P0+0.01,d0]); close all %titul='Sensibilidad a las condiciones iniciales (s3)'; %figure('Name',titul),plot(t3, solnum3(:,1).^2); %axis tight, title(titul), xlabel('t'), ylabel('F^2') %titul='Sensibilidad a las condiciones iniciales (s4)'; %figure('Name',titul),plot(t4, solnum4(:,1).^2); %axis tight, title(titul), xlabel('t'), ylabel('F^2') titul='Sensibilidad a las condiciones iniciales (3vs4)'; figure('Name',titul),plot(t3, solnum3(:,1).^2, t4, solnum4(:,1).^2); axis tight, title(titul), xlabel('t'), ylabel('F^2'), legend('solnum3','solnum4') tmin=0; tmax=50; nmin=find(t3>=tmin,1,'first'); nmax=find(t3<=tmax,1,'last'); titul='Sensibilidad a las condiciones iniciales (s3^2-s4^2)'; figure('Name',titul),plot(t3(nmin:nmax), solnum3(nmin:nmax,1).^2 - solnum4(nmin:nmax,1).^2); axis tight, title(titul), xlabel('t'), ylabel('F_3^2-F_4^2') % titul='Sensibilidad a las condiciones iniciales 3D (s3)'; % figure('Name',titul),plot3(solnum3(:,1), solnum3(:,2),-solnum3(:,3)); % axis tight, title(titul), xlabel('F'), ylabel('P'), zlabel('-d') % titul='Sensibilidad a las condiciones iniciales 3D (s4)'; % figure('Name',titul),plot3(solnum4(:,1), solnum4(:,2),-solnum4(:,3)); % axis tight, title(titul), xlabel('F'), ylabel('P'), zlabel('-d') tmin=0; tmax=20; nmin=find(t3>=tmin,1,'first'); nmax=find(t3<=tmax,1,'last'); titul='Sensibilidad a las condiciones iniciales 3D (3vs4)'; figure('Name',titul),plot3(solnum3(nmin:nmax,1), solnum3(nmin:nmax,2),-solnum3(nmin:nmax,3), solnum4(nmin:nmax,1), solnum4(nmin:nmax,2),-solnum4(nmin:nmax,3)); axis tight, title(titul), xlabel('F'), ylabel('P'), zlabel('-d'), legend('solnum3','solnum4')
close all